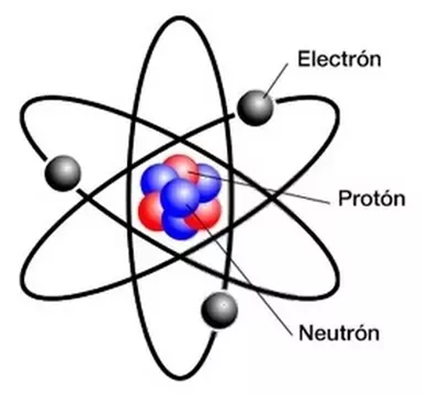
Todo el proceso eléctrico comienza desde el entendimiento de la misma estructura del átomo. La estructura atómica que se conoce en la actualidad es al siguiente:

Se ha descubierto que existen dos tipos de carga: las positivas y las negativas. La positiva es transportada por los protones y la negativa por los electrones. La carga de un protón es demasiado pequeña como para ser tenida en cuenta como unidad básica de carga. La unidad de carga en el SI es el COULOMB ( C ). El símbolo para representar una cantidad de carga constante es Q, y el de una carga que varía con el tiempo q. La carga eléctrica de un electrón es de -1,602*10^{-9 C. Cuando el átomo se excita, puede perder o
ganar electrones. Cuando el átomo pierde electrones, hay mas cargas positivas
que negativas. Se dice que el átomo esta cargado positivamente o tiene un
potencial positivo. Es lo que se denomina ión positivo.}

Cuando el átomo gana electrones, hay mas cargas negativas que positivas. Se dice que el átomo esta cargado negativamente o tiene un potencial negativo. Es lo que se denomina ión negativo.

Los electrones que están más cerca del núcleo experimentan mayor fuerza de atracción que los que están en las órbitas exteriores, la naturaleza de esa atracción es lo que define la dureza de los materiales que se conocen. Se puede concluir que POTENCIAL es el estado eléctrico del átomo y puede ser neutro, positivo o negativo. El potencial de un átomo se determina con el solo hecho de hallar la diferencia entre el número de protones y electrones del mismo. Cuando los átomos de dos materiales diferentes tienen potenciales diferentes, esa diferencia de potencial es lo que se denomina TENSIÓN, VOLTAJE O F.E.M. ( FUERZA ELECTROMOTRIZ ). En otras palabras, se crean las condiciones para el intercambio de electrones.

Los electrones que se encuentran en las órbitas más alejadas del núcleo se les conoce también como electrones libres. Dichos electrones son los responsables de la mayoría de los fenómenos eléctricos ya que al estar débilmente atraídos por los protones del núcleo, pueden moverse fácilmente de un átomo a otro.

1.2. TENSION O FEM

La tensión o fuerza electromotriz entre dos puntos ( también llamado diferencia de potencial o fuerza electromotriz ) es el trabajo requerido en Joul para mover una carga de 1 C de un punto a otro. Se puede entender como la fuerza que se establece entre dos puntos debido a una diferencia de potenciales de los mismos que tiende a mover electrones de un lado al otro hasta el equilibrio eléctrico. Se mide en voltios

TENSION ( Voltios ) = ( W ( Joul ) / Q ) = I * R

1.2.1. TENSION DIRECTA

La fuente de tensión directa posee dos polos: uno positivo ( ánodo ) por donde salen los electrones y uno negativo ( cátodo ) por donde llegan los electrones después de hacer el recorrido por el circuito. Una fuente de tensión de corriente directa, como su nombre lo indica, genera corriente directa, por ejemplo en el caso de las pilas y baterías y dispositivos electrónicos.

En resumen las fuentes de tensión directa:

1.2.2. TENSION ALTERNA

Una fuente de tensión alterna, como su nombre lo indica, genera corriente alterna, debido a que cambia su polaridad con el tiempo; por ejemplo en el caso de las transmisiones de alta y baja potencia, circuitos de casa.

En resumen, en las fuentes de tensión alterna:

El valor de la tensión de operación de equipos que funcionan con tensión alterna esta en la placa de información del mismo:

1.3. CORRIENTE ELECTRICA O INTENSIDAD ( I )

La corriente eléctrica se obtiene como consecuencia del movimiento de cargas eléctricas y se define como la cantidad de carga que pasa por unidad de tiempo. En otras palabras, es un movimiento de electrones a través de un conductor.

I ( amperios ) = Q / tiempo

Otra definición puede ser como el flujo de cargas eléctricas que transporta la energía desde la fuente hasta el destinatario.

1.3.1. CIRCUITO DE CORRIENTE DIRECTA ( DC )

En el circuito de corriente directa, que se asocia a una fuente de tensión directa ( DCV ) , los electrones salen del lado positivo de la fuente ( ánodo ) y recorren el circuito para llegar al lado negativo de la fuente ( cátodo ), dicho movimiento se mantiene inalterado en el tiempo, en el mismo sentido, se dice entonces que el circuito es de corriente directa. Su grafica en el tiempo es:

Si la fuente invierte la polaridad, entonces los electrones cambian el sentido de movimiento:

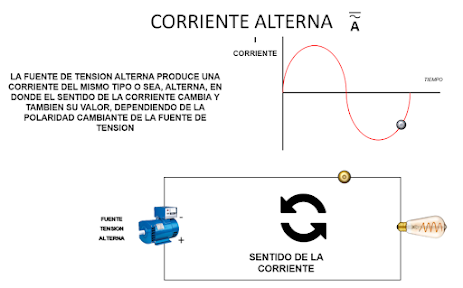
1.3.2. CIRCUITO DE CORRIENTE ALTERNA ( AC )

En el circuito de corriente alterna, que se asocia a una fuente de tensión alterna ( ACV ) , los electrones salen de un lado de la fuente y recorren el circuito para llegar al otro lado de la fuente, y después se devuelven; su movimiento se mantiene cambiando en el tiempo de un sentido a otro, en otras palabras, la corriente alterna cambia su sentido de movimiento en el tiempo, cambia el valor de corriente y cambia el valor de tensión de la fuente; se dice entonces que el circuito es de corriente alterna. Su grafica en el tiempo es:

La corriente alterna tiene como características:

· En el ciclo tiene tres instantes en donde el valor de la corriente es cero ( 0 ).

· Tiene dos instantes en donde la corriente alcanza su máximo valor.

· Cambia su sentido de movimiento dos veces en el ciclo.

El valor de la corriente en un equipo viene especificado en la placa de datos del mismo:

Con relación a la onda alterna de tensión, se tienen los siguientes conceptos básicos que veremos más adelante:

1.4. RESISTENCIA ELECTRICA

Es la resistencia u oposición que opone un material al flujo de una corriente eléctrica.

La resistencia de un material depende de varias propiedades:

R = r L / A

r: Coeficiente resistividad del material ( Ohm – mts )

L: Longitud del conductor ( mts )

A: Área sección transversal conductor ( mts² )

Vemos que la resistencia es inversamente proporcional a la corriente; o sea, que si hay mayor resistencia en un circuito, la corriente que pasa por el mismo disminuye; si la resistencia del circuito es baja, la corriente del mismo se incrementa.

1.5. LEY DE OHM

La ley de ohm relaciona la tensión, la corriente y la resistencia en una formula, aplicada a circuitos resistivos:

TENSION = CORRIENTE * RESISTENCIA

V = I * R I = V / R R = V / I

De la anterior fórmula se deduce que:

· Si la carga requiere mayor corriente, se requiere de mayor tensión de la fuente y viceversa manteniendo un valor constante de resistencia.

· Si la carga tiene alta resistencia, se necesita de mayor tensión para poder hacer circular los electrones y viceversa.

1.6. POTENCIA EN SISTEMAS DC

Es la rapidez con que se genera o se consume energía, generalmente en forma de calor. La potencia es lo que requieren las unidades o artefactos eléctricos en función de corriente y voltaje para poder funcionar y no varia en el tiempo. También se puede definir como la capacidad que tiene la electricidad para producir trabajo en un tiempo dado.

P ( Watt ) = ( Trabajo / tiempo ) = V (Q / t ) = ( V I ) = ( I² R ) = ( V² / R )

La unidad de potencia común es el WATT, pero también se expresa en KWatt.

1.6.1. POTENCIA ENTREGADA

Es la potencia en función de la tensión y corriente que suministra o aporta una fuente, como las baterías e inclusive un transformador. Las fuentes de voltaje aportan un voltaje fijo y la corriente que requiere el elemento eléctrico o carga en este caso; o sea que la potencia que entrega la fuente es variable y depende del elemento que se conecta a la misma.

1.6.2. POTENCIA CONSUMIDA

Es la potencia en función de la tensión y corriente que necesitan o consumen los artículos eléctricos en el tiempo para funcionar u operar. La fuente de voltaje debe poder la potencia necesaria requerida por el elemento eléctrico para poder funcionar correctamente, por tanto se deduce que para los sistemas eléctricos:

POTENCIA SUMINISTRADA >= POTENCIA CONSUMIDA

En los equipos eléctricos , este valor está en la placa de información del mismo:

1.7. ENERGIA ELECTRICA

Recordando los principios de física se definía que:

Potencia = ( Trabajo o energía ) / tiempo, despejando de la ecuación se tiene:

Energía ( Watt – hora ) = Potencia * Tiempo

Lo que vende la compañía de electricidad a nuestras casas es la energía que consumen lo elementos eléctricos en un mes. Esta energía se calcula sumando la potencia de cada uno de los aparatos por su tiempo de funcionamiento en horas durante el mes:

Energía Consumida = Total Potencia eléctrica * Tiempo operación en horas durante el mes

Si desea saber el costo de esta energía se realiza el siguiente cálculo:

Costo Energía Periodo = Energía Consumida Periodo * Valor del Kwatt – Hr

Costo energía Periodo = Total Potencia eléctrica * Tiempo operación en horas durante el mes * Valor Kwatt-Hr

La energía es la base del cálculo para el consumo y diseño de sistemas de alimentación eléctrica.

Veamos un ejemplo de cálculo de energía y de costos de operación

Tomemos por ejemplo el caso de esta cafetera, y se determinan los parámetros eléctricos:

Ahora se procede a calcular la corriente del equipo:

Recordando que:

P = Tensión * Corriente = V * I

Podemos encontrar el valor de la corriente I del equipo mediante la fórmula:

I = P ( Watt ) / T ( Voltios )

Reemplazando los valores en la ecuación:

I = P ( Watt ) / T ( Voltios )

I = 600 Watts / 120 Voltios = 5 Amperios

Para estimar el costo de operación de este equipo por mes, lo primero que hay que calcular es la energía que se consume el equipo por mes, para eso se necesita conocer su potencia de consumo eléctrico ( 600 watts ) y las horas estimadas de operación del equipo por mes para obtener el valor de la energía con la fórmula:

Energía consumida = Potencia eléctrica consumo * Tiempo ( Horas )

Supongamos que el equipo lo operamos por dos ( 2 ) horas por día de lunes a sábado, entonces el tiempo estimado de operación en horas por mes es de :

Tiempo operación en Hrs/Mes = Horas uso/Día * Días de operación

Como en la semana se usan 6 días, y son cuatro semanas del mes, entonces los días de operación son 6 *4 = 24 días, reemplazando en la formula:

Tiempo operación Hrs/Mes = 2 Horas/Día * 24 Días = 48 Hrs/Mes

Teniendo los valores de la potencia en Watts ( 600 Watts ) del equipo y el tiempo de operación en Hrs/Mes ( 48 Hrs/Mes ) se obtiene el valor de la energía consumida por mes, reemplazando en la fórmula:

Energía consumida/Mes = Potencia eléctrica consumo * Tiempo operación en Hrs/Mes

Reemplazando en la fórmula los valores:

Energía consumida/Mes = 600 Watts * 48 en Hrs/Mes

Energía consumida/Mes = 28800 Watt-Hr/Mes

Para efectos prácticos, se convierte la unidad de Watt-Hr/Mes a Kwatts-Hr/Mes, dividiendo el valor entre 1000, por tanto:

Energía consumida/Mes = 28,800 KWatt-Hr/Mes

Recordado que el costo o valor de la factura de energía esta en función de la fórmula:

Valor del consumo por mes = CONSUMO DE ENERGIA POR MES EN KWATT – HR/Mes * Valor tarifa del Kwatt-Hr ($/Kwatt-Hr )

Con base en el valor o tarifa del Kwatt-Hr que tiene el distribuidor de energía, que viene en la factura:

Reemplazado en la fórmula:

Valor del consumo por mes = 28,8 KWATT HR/Mes * $ 566,58/ Kwatt-Hr

Valor del consumo por mes = $16317,5/Mes

Puede hacer un cuadro que le facilite los cálculos para usar en una matriz Excel, como se observa a continuación:

Ahora si los equipos traen la ficha de eficiencia energética, el cálculo es mucho más fácil y sencillo, para ello analicemos la información que usaremos de la ficha:

Para estimar el valor del consumo de operación de este equipo por mes, tenga en cuanta los valores de:

CONSUMO PROMEDIO DE ENERGIA POR MES EN KWATT – HR = 100,8 Kwatt-Hr / Mes

Y con base en el valor o tarifa del Kwatt-Hr que tiene el distribuidor de energía, que viene en la factura:

Recordando la fórmula:

Valor del consumo por mes = CONSUMO PROMEDIO DE ENERGIA POR MES EN KWATT – HR/Mes * Valor tarifa del Kwatt-Hr ($/Kwatt-Hr )

Reemplazado los valores en la fórmula:

Valor del consumo por mes = 100,8 KWATT HR/Mes * $ 566,58/ Kwatt-Hr

Valor del consumo por mes = $57111.26/Mes

Si dese usar un cuadro de cálculo, es mas sencillo y se muestra a continuación:

Ver videos:

ESTIMACION O CALCULO DE LA ENERGIA CONSUMIDA Y COSTO DE FACTURA EN EQUIPOS ELECTRICOS

UNIDADES ELECTRICAS ( TENSION, CORRIENTE, RESISTENCIA , POTENCIA ELECTRICA , ENERGIA ) Y LEY DE OHM

1.8. USO DE MULTIMETROS, PINZAS AMPERIMETRICAS.

Los instrumentos más usados son el multímetro, la pinza amperimétrica y el secuencímetro; comenzaremos analizando el multímetro:

Es el instrumento de mayor uso, se usa para medición de voltajes AC y DC, resistencias y algunos parámetros especiales como frecuencias, temperaturas, capacitancia, etc.

Entre las partes que constituyen el multímetro están:

Para medir tenga en cuenta:

· El parámetro que va a a medir

· Verificar la correcta posición de las puntas de medición.

· Colocar el selector en la escala adecuada para medir.

· Leer correctamente el valor mostrado en el display.

En la actualidad hay multímetro auto escalables, por tanto no es necesario el ajuste manual de la escala, obviamente son un poco más costosos, pero muy versátiles; y también están los inteligentes que ellos mismos seleccionan la variable a medir y su escala

Debido a que en la mayoría de los display tienen capacidad para máximo 4 dígitos, estos instrumentos se ayuda de prefijos matemáticos, para expresar valores con mas de 4 dígitos, entre los más comunes están:

OBS: Muchos de ellos vienen para medir corrientes, pero recomiendo no hacerlo con este instrumento sino, con una pinza amperimétrica.

Ahora vemos ejemplos para medir, los primero es colocar las puntas de prueba en sus respectivos lugares:

Para medir resistencias o continuidad, asegúrese previamente que el equipo no este energizado, coloque el selector en el cuadrante de resistencia y en la escala apropiada para una medición precisa:

Para la medición de tensión de tipo DC, coloque el selector en el cuadrante de resistencia y en la escala apropiada para una medición precisa:

Para la medición de tensión de tipo AC, coloque el selector en el cuadrante de resistencia y en la escala apropiada para una medición precisa:

Ver video:

OPERACIÓN DEL MULTIMETRO DIGITAL

Seguimos ahora analizando la pinza amperimétrica. Con este instrumento especializado en medir corrientes de tipo AC y DC, también podemos medir voltajes AC y DC, así como resistencias y otros parámetros como temperaturas, frecuencias, etc.

Para medir tenga en cuenta:

· El parámetro que va a medir.

· Verificar si se requiere conectar las puntas de prueba ( no se emplean cuando se miden corrientes )

· Verificar la correcta posición de las puntas de medición.

· Colocar el selector en la escala adecuada para medir.

· Leer correctamente el valor mostrado en el display.

En la actualidad hay pinzas autoescalables, por tanto no es necesario el ajuste manual de la escala, obviamente son un poco más costosos, pero muy versátiles:

Para medir resistencias o continuidad, asegúrese previamente que el equipo no este energizado, coloque el selector en el cuadrante de resistencia y en la escala apropiada para una medición precisa:

Para la medición de tensión de tipo DC, coloque el selector en el cuadrante de resistencia y en la escala apropiada para una medición precisa:

Para la medición de tensión de tipo AC, coloque el selector en el cuadrante de resistencia y en la escala apropiada para una medición precisa:

Para la medición de corriente AC, coloque el selector en el cuadrante y escala para una medición precisa y coloque un solo cable en el centro de las pinzas:

Para la medición de corriente DC, coloque el selector en el cuadrante y escala para una medición precisa y coloque un solo cable en el centro de las pinzas, pero tenga en cuenta el signo en el display:

No realice las siguientes acciones:

Ver video:

OPERACION DE LA PINZA AMPERIMETRICA

1.9. ANALISIS DE CIRCUITOS DC

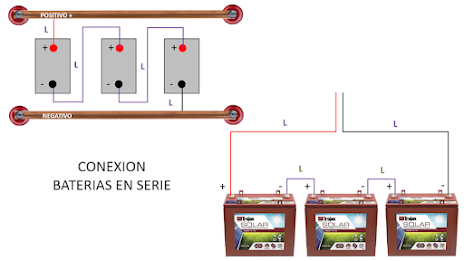
1.9.1. FUENTES DE TENSION DC EN SERIE.

La conexión de fuentes de tensión en serie es un polo a continuación de otro; o sea, un polo positivo de una fuente con el negativo de la otra fuente, tal como se muestra en el esquema:

La tensión que se marca entre los puntos A y b es de 10 V, por lo tanto se puede deducir que si se tienen N fuentes de tensión conectados en serie, el valor de voltaje total de dichas fuentes en serie es de:

V_TOTAL = V₁ + V₂ + … + V_N

La corriente que pasa por las fuentes de tensión DC en serie es la misma para cada una de ellas y dependen de la carga del circuito.

Para entender el proceso, vamos a hacer la analogía con dos electrobombas y veamos sus parámetros comparados con una fuente de tensión DC:

Para el caso, el flujo de agua de la bomba equivale a la corriente de la fuente y la presión de la bomba equivale a la tensión de la fuente. Ahora vamos a hacer una conexión serie:

En el caso anterior, el flujo de agua que entra en una bomba, es el mismo que entra en la otra, lo que equivale a decir que en las fuentes en serie la corriente que entra en una de ellas es la misma que entra y sale de la otra; por tanto fuentes de tensión en serie tienen igual corriente. Ahora analicemos las presiones y tensiones en ambos casos:

En el caso de las bombas, el líquido que entra en la primera bomba, experimenta una incremento de la presión y cuando entra en la otra incrementa nuevamente la presión, por tanto en las fuentes de tensión en serie se incrementa el valor de voltaje del sistema. Por tanto:

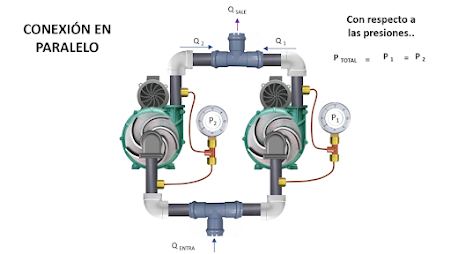
1.9.2. FUENTES DE TENSION DC EN PARALELO.

En este tipo de conexión, se conectan los polos positivos de todas las fuentes y los polos negativos de todas las fuentes, tal como se ve en el esquema:

El valor de tensión que se marca entre los puntos A y b es de 6 V, por lo tanto, se puede deducir que si se tienen N fuentes de tensión, el valor del voltaje total de dichas fuentes en serie es de:

V_TOTAL = V₁ = V₂ = … = V_N

La corriente total de las fuentes en paralelo, se construye con la corriente que aporta cada fuente en paralelo, por tanto se puede decir que la corriente total de las fuentes en paralelo es la suma de cada corriente aportada por cada fuente:

I_TOTAL = I₁ + I₂ + …+ I_N

Para entender esta nueva condición, analicemos nuevamente el caso de las bombas:

Para el caso, cada bomba maneja un caudal independiente que se unen al caudal del resto del as otras bombas, ósea, que el caudal total está constituido por el aporte o suma de cada una de las bombas que componen el arreglo. Para el caso de las baterías:

La corriente total del arreglo es la suma de las corrientes aportadas por las baterías. Ahora para que esto se puede cumplir sin problemas, las presiones de las bombas deben ser iguales, porque si una es mayor le inyectara agua a la otra, lo que equivale a decir que, en las fuentes, todas deben tener el mismo nivel de tensión porque si una está más baja, las demás van a cargarla.

La ventaja de las fuentes en paralelo es que como cada una aporta una menor corriente, demoran mucho más tiempo funcionando.

En el caso de sistemas mixtos, la regla para su análisis es:

· Tenga a la mano la información del valor de tensión y corriente de las fuentes que intervienen en el arreglo.

· Identifique el ramal básico que componen el arreglo, este ramal tiene todas las fuentes en serie y conectadas.

· Calcule el valor de tensión de este ramal , String o subarreglo; el valor de este ramal se constituye en el valor del voltaje del arreglo total, ya que los demás ramales están en paralelo.

· Sume ahora las corrientes que aportan el resto de ramales para hallar la cantidad de corriente que aporta el arreglo.

· Puede calcular la potencia de arreglo, ya sea sumando las potencias de todas las fuentes que conforman el arreglo realizando la multiplicación del valor de tensión total del arreglo por la corriente total del arreglo.

Ver video:

ANALISIS DE FUENTES DC EN CONFIGURACION O ARREGLOS SERIE PARALELOS Y MIXTOS

1.9.3. RESISTOR

Es el componente de un circuito que se usa debido a su resistencia. Generalmente un resistor emite calor cuando pasa corriente a través de él.

1.9.3.1. POTENCIA CONSUMIDA POR UN RESISTOR.

La potencia de un resistor esta representada por el calor que emite el mismo.

P = I² R = ( V² / R ) = V I

Como se puede observar, si se incrementa la corriente en el circuito, la energía consumida por unidad de tiempo ( Potencia ) se incrementa.

1.9.3.2. RESISTORES EN SERIE

Los resistores en serie se identifican porque:

· La corriente que entra en uno de ellos es la misma para los otros.

· Generalmente las resistencias en serie tienen diferentes valores de tensión. La tensión de la fuente se reparte entre las diferentes resistencias en serie de acuerdo a la resistencia de cada una.

· Donde finaliza una comienza la otra.

Por lo expresado anteriormente se concluye que para resistencias en serie:

I _TOTAL = I ₁ = I ₂ = I_N

TENSION _FUENTE = V ₁ + V ₂ + … + V _N

Por la ley de Ohm:

( I _TOTAL * R _T ) = ( I ₁ * R ₁ ) + ( I ₂ * R ₂ ) + … + ( I _N * R _N )

Pero como las corrientes son iguales, la ecuación quedará:

Para resistores colocados en serie, su resistor equivalente quedaría:

R _EQUIVALENTE = R₁ + R₂ + ..+ R_N

En otras palabras, resistencias conectadas en serie se comportan como una sola con la suma de los valores de las resistencias del circuito original, por tanto, la corriente del circuito disminuye debido a que hay mayor resistencia en el mismo.

Se puede definir la resistencia equivalente como aquella resistencia que permite obtener la misma corriente total que se obtendría con el arreglo de resistencias en el circuito. Veamos el siguiente ejemplo:

Con respecto a las potencias consumidas con la aportada por la fuente de voltaje se tiene:

V _FUENTE = V ₁ + V ₂ + … + V _N

Si se multiplica la anterior ecuación por la corriente total que es común a todas se tiene que:

( I _TOTAL * V _FUENTE ) = ( I _TOTAL * V ₁ ) + ( I _TOTAL * V ₂ ) + … + ( I _TOTAL * V _N )

Potencia fuente = P ₁ + P ₂ + ... + P _N

1.9.3.3. RESISTORES EN PARALELO

Las resistencias en paralelo se conocen porque:

· Tienen o reciben la misma tensión.

· Generalmente poseen distintos valores de corriente.

· Las resistencias en paralelo comienzan en un mismo punto y finalizan en un mismo punto.

I _TOTAL = I ₁ + I ₂ +…+ I_N

TENSION _FUENTE = V ₁ = V ₂ = … = V _N

Por la ley de Ohm se tiene que:

( V _FUENTE / R _T ) = ( V ₁ / R ₁ ) + ( V ₂ / R ₂ ) +…+ ( V _N / R _N )

( 1 / R _T ) = ( 1 / R ₁ ) + ( 1 / R ₂ ) +…+ ( 1 / R _N )

R _EQUIVALENTE = 1 / [ ( 1 / R₁ ) + ( 1 / R₂ ) + ..+ ( 1 / R_N ) ]

Para resistores en paralelo:

R _EQUIVALENTE = 1 / [ ( 1 / R₁ ) + ( 1 / R₂ ) + ..+ ( 1 / R_N ) ]

En otras palabras, resistencia conectadas en serie se comportan como una sola con un valor de resistencia menor que cualquiera de ellas, por lo tanto, la corriente que pasa por el circuito se incrementa. Con respecto a las potencias consumidas con la aportada por la fuente de voltaje se tiene:

I _TOTAL = I ₁ + I ₂ + … + I _N

Si se multiplica la anterior ecuación por el voltaje de la fuente que es común a todas se tiene que:

( I _TOTAL * V _FUENTE ) = ( I ₁ * V _FUENTE ) + ( I ₂ * V _FUENTE ) + … + ( I _N * V _FUENTE )

Pot fuente = P ₁ + P ₂ + .. + P _N

Veamos el siguiente ejemplo:

Ver video:

CONEXION, ANALISIS Y COMPORTAMIENTOS DE RESISTENCIAS EN SERIE Y PARALELOS EN CIRCUITOS DC

1.9.4. CAPACITORES Y CAPACITANCIA

Un condensador o capacitor es un dispositivo almacenador de energía en la forma de un campo eléctrico. El capacitor consiste de dos placas, que están separadas por un material aislante, que puede ser aire u otro material "dieléctrico", que no permite que éstas (las placas) se toquen. Se parece a la batería que todos conocemos, pero el condensador solamente almacena energía, pues no es capaz de crearla. Los condensadores se miden en Faradios (F.), pudiendo encontrarse condensadores que se miden en Microfaradios (uF), Pico faradios (pF) y Nanofaradios (nF). A continuación, se pueden ver algunas equivalencias de unidades.

El primer capacitor es la botella de Leyden, el cual es un capacitor simple en el que las dos placas conductoras son finos revestimientos metálicos dentro y fuera del cristal de la botella, que a su vez es el dieléctrico. La magnitud que caracteriza a un capacitor es su capacidad, cantidad de carga eléctrica que puede almacenar a una diferencia de potencial determinado. La botella de Leyden, uno de los Capacitores más simples, almacena una carga eléctrica que puede liberarse, o descargarse, juntando sus terminales, mediante una varilla conductora. La primera botella de Leyden se fabricó alrededor de 1745, y todavía se utiliza en experimentos de laboratorio. Hay muchas formas de capacitares y pueden clasificarse de acuerdo al tipo de material dieléctrico que se usa entre las placas conductoras. Para aplicaciones de circuitos electrónicos, el material dieléctrico puede ser aire, vacío, papel impregnado de aceite, plástico, etc.

Para un capacitor se define su capacidad como la razón de la carga que posee uno de los conductores a la diferencia de potencial entre ambos, es decir, la capacidad es proporcional al la carga e inversamente proporcional a la diferencia de potencial: C = Q / V, medida en Farad (F). La diferencia de potencial entre estas placas es igual a: V = E * d ya que depende de la intensidad de campo eléctrico y la distancia que separa las placas. También: V =q / e * d, siendo q carga por unidad de superficie y d la diferencia entre ellas. Para un capacitor de placas paralelas de superficie S por placa, el valor de la carga en cada una de ellas es q * S y la capacidad del dispositivo:

C = q * S / (q * d / e ) = e * S / d Siendo d la separación entre las placas.

La energía acumulada en un capacitor será igual al trabajo realizado para transportar las cargas de una placa a la otra venciendo la diferencia de potencial existente ellas:

D W = V * D q = (q / C) * D q

La energía electrostática almacenada en el Capacitor será igual a la suma de todos estos trabajos desde el momento en que la carga es igual a cero hasta llegar a un valor dado de la misma, al que llamaremos Q.

W = V * dq = ( 1 / C) * ( q * dq) = 1 / 2 (Q2 / C)

Si ponemos la carga en función de la tensión y capacidad, la expresión de la energía almacenada en un capacitor será: W = 1/2 * C * V2 medida en unidades de trabajo. Dependiendo de superficie o área de las placas su fórmula de capacidad es

C = e * A / 4p d, donde e es la constante dieléctrica.

1.9.4.1. CAPACITANCIA

Es la propiedad eléctrica de los condensadores y la medida de su capacidad para almacenar carga en sus dos conductores. La unidad de la Capacitancia en el SI es el FARADIO ( F ). Pero para aplicaciones prácticas se emplea el micro faradio o mF. C = Q / V

1.9.4.2. ENERGIA ALMACENADA EN UN CAPACITOR

La energía almacenada en un capacitor está en función de su capacitancia y de la tensión aplicada al mismo, mediate la fórmula:

W_CAPACITOR = ( ½ ) C V²

1.9.4.3. COMPORTAMIENTO DE UN CAPACITOR EN UN CIRCUITO DC.

Lo que indican las graficas, es que la tensión en un capacitor con el tiempo se estabiliza, o sea, que este elemento es un regulador de tensión de un circuito, pero también la corriente que pasa a través de él tiene a cero, o sea, que se comporta con una circuito abierto.

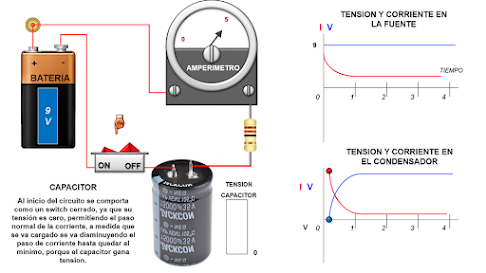
Al inicio del circuito se comporta como un switch cerrado, ya que su tensión es cero, permitiendo el paso normal de la corriente, a medida que se va cargado se va disminuyendo el paso de corriente hasta quedar al mínimo, porque el capacitor gana tensión:

Después de un tiempo:

1.9.4.4. PROCESO DE CARGA DE UN CAPACITOR EN SISTEMAS DC

El proceso de carga de un capacitor conectado en serie con una resistencia viene dado por la expresión:

Vc = Vf + ( Voc – Vf )* e^{- RC/ t}

Donde:

Vf : Tensión de la fuente.

Voc : Tensión inicial del condensador

t : Tempo en segundos.

R: Resistencia en ohmios.

C: Capacitancia en faradios

La corriente que pasa por el condensador está expresada por la ecuación:

Ic = [ ( Vf – Voc )* e^{- RC/ t} ] / R

1.9.4.5. PROCESO DE DESCARGA DE UN CAPACITOR

En este caso, al cerrar el circuito, el capacitor se descarga, y en ese proceso pasa de tener una alta tensión y corriente a una tensión y corriente de valores de cero.

Al tiempo:

Como desaparece la tensión de la fuente, o es igual a cero, para el proceso de descarga de un condensador, las ecuaciones de la carga quedan modificadas de la siguiente forma:

Vc = Voc * e^{- RC/ t}

Ic = [ – Voc * e^{- RC/ t} ] / R

Ver video:

COMPORTAMIENTO DE LOS CAPACITORES O CONDENSADORES ANTE TENSIONES Y CORRIENTES DC

1.9.4.6. CAPACITORES EN SERIE EN SISTEMAS DC

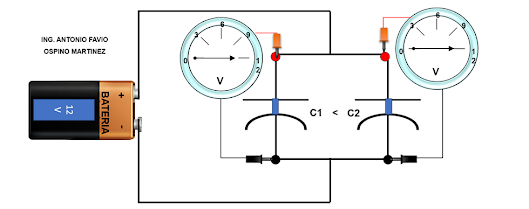
Con relación al comportamiento de los capacitores en conexión serie, al energizar el circuito, los capacitores están descargados y se comportan como interruptores cerrados dejando para la corriente plena sin problemas:

A medida que comienzan a cargarse, ganan tensión y comienzan a restringir el flujo de corriente; el capacitor con menos capacitancia gana más tensión en comparación con el capacitor con mayor valor de capacitancia.

Después de un tiempo, la suma de las tensiones de los capacitores tendrán un valor muy cercano al valor de la fuente y dejan pasar una corriente muy cercana a cero ( 0 ), comportándose al final como interruptores abiertos:

Cuando se tienen capacitores en serie, se pueden reemplazar todos ellos por uno solo que nos dé las mismas características de operación del circuito; para el caso de estos componentes se cumple que, para conexiones en serie:

Veamos el siguiente ejemplo:

1.9.4.7. CAPACITORES EN PARALELO EN SISTEMAS DC

En relación, al comportamiento de los capacitores en paralelo, al energizar el circuito, los capacitores están descargados y se comportan como interruptores cerrados dejando para la corriente plena sin problemas:

A medida que comienzan a cargarse, ganan tensión y comienzan a restringir el flujo de corriente; el capacitor con menos capacitancia gana tensión con mayor rapidez en comparación con el capacitor con mayor valor de capacitancia

Después de un tiempo, ambos capacitores tendrán una tensión muy cercana al valor de la fuente y dejan pasar una corriente muy cercana a cero ( 0 ), comportándose al final como interruptores abiertos

Cuando se tienen capacitores en paralelo, se pueden reemplazar todos ellos por uno solo que nos dé las mismas características de operación del circuito; para el caso de estos componentes se cumple que, para conexiones en paralelo:

Veamos el siguiente ejemplo:

Ver video:

CONEXION, ANALISIS Y COMPORTAMIENTO DE CAPACITORES EN SERIE Y PARALELO EN SISTEMAS DC

1.9.5. INDUCTORES E INDUCTANCIA

Junto al capacitor, otro elemento que almacena energía es el Inductor ó bobina, que es básicamente un alambre enrollado sobre sí mismo, donde el material de su centro, es de aire y en otras ocasiones es de un material diferente, que posee un grado de permeabilidad. Como en el capacitor las cualidades de este elemento, dependen de su forma geométrica y física, y presenta la propiedad de la inductancia, que es la característica de un material de almacenar energía, en el campo magnético generado por la variación de corriente que lo atraviesa. Una característica interesante de las bobinas es que se oponen a los cambios bruscos de la corriente que circula por ellas. Esto significa que a la hora de modificar la corriente que circula por ellas (ejemplo: ser conectada y desconectada a una fuente de poder), esta tratará de mantener su condición anterior.

Las bobinas se miden en Henrios (H.), pudiendo encontrarse bobinas que se miden en Mili henrios (mh). El valor que tiene una bobina depende de:

· El número de espiras que tenga la bobina (a más vueltas mayor inductancia, o sea mayor valor en Henrios)

· El diámetro de las espiras (a mayor diámetro, mayor inductancia, o sea mayor

valor en Henrios).

· La longitud del cable de que está hecha la bobina.

· El tipo de material de que esta hecho el núcleo si es que lo tiene.

1.9.5.1. FLUJO MAGNÉTICO

Los fenómenos magnéticos se explican mediante el concepto de flujo magnético. La unidad de flujo en el SI es el WEBER ( Wb ). El símbolo para una cantidad de flujo constante es F, y para un flujo variable se emplea f. La corriente que circula por un alambre también produce un flujo, con el reglamento de la mano derecha. El mismo fenómeno se obtiene al colocar un material ferromagnético en el interior y alrededor de esta estructura llamada bobina. El término PERMEABILIDAD, cuyo símbolo es m, es una medida de esta propiedad que hace aumentar el flujo; su unidad en el SI es el HENRY/MTS y su símbolo unitario es H/m. la permeabilidad del vacío, m₀ , es de 0,4 p m H/m. En la mayor parte de las bobinas, una corriente i produce un eslabonamiento de flujo Nf que es proporcional a i. La inductancia de una bobina depende de la forma de la bobina misma, de la permeabilidad del material que la rodea, del número de vueltas, del espaciamiento entre las vueltas y otros factores:

L = N² m A / l

N: Numero vueltas alambre

m: Permeabilidad magnética del núcleo.

A: Area sección transversal del núcleo.

l : Longitud bobina en metros.

1.9.5.2. COMPORTAMIENTO DE UN INDUCTOR EN UN CIRCUITO DC.

Cuando se conecta un inductor a un circuito, la tensión en él tiende a cero ( 0 ) mientras que la corriente va de cero a un valor establecido, por lo cual el inductor es un regulador de corriente y al cargarse deja el circuito cerrado.

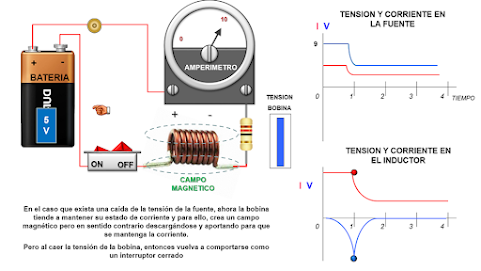
Al energizar el circuito, la bobina se comporta como un switch abierto, debido a que en ese momento, la bobina crea una tensión momentánea para oponerse al flujo de corriente de forma que impide el paso de la misma, a medida que pasa el tiempo, su tensión se cae, permitiendo el paso de mayor corriente.

Al final se comporta como un switch cerrado, permitiendo el paso de corriente y la formación del campo magnético.

Después de un tiempo:

En el caso que exista una caída de la tensión de la fuente, ahora la bobina tiende a mantener su estado de corriente y para ello, crea un campo magnético pero en sentido contrario descargándose y aportando para que se mantenga la corriente. Pero al caer la tensión de la bobina, entonces vuelva a comportarse como un interruptor cerrado

Al tiempo:

Ver video:

COMPORTAMIENTO DE INDUCTORES O BOBINAS ANTE TENSIONES Y CORRIENTES DC

1.9.5.3. INDUCTORES EN SERIE EN SISTEMAS DC

Con relación, al comportamiento de inductores en serie, al energizar el circuito, para oponerse a la corriente, ambas bobinas crean una tensión proporcional al valor de inductancia de cada una de ellas cuya suma da el valor de tensión de la fuente:

A medida que comienzan a perder esa tensión, comienzan a conducir más y más corriente; la bobina con menos inductancia y menor tensión, pierde esa tensión opositora con mayor rapidez en comparación con la bobina de mayor inductancia

Después de un tiempo, ambas bobinas tendrán una tensión muy cerca los 0 voltios y dejan pasar la corriente plena:

Cuando se tienen inductores en serie, se pueden reemplazar todos ellos por uno solo que nos dé las mismas características de operación del circuito; para el caso de estos componentes se cumple que, para conexiones en serie:

Veamos el siguiente ejemplo:

1.9.5.4. INDUCTORES EN PARALELO EN SISTEMAS DC

Con relación a comportamiento de los inductores en paralelo, al energizar el circuito, para oponerse a la corriente, ambas bobinas crean una tensión de igual capacidad a la de la fuente:

A medida que comienzan a perder esa tensión, comienzan conducir mas y mas corriente; la bobina con menos inductancia, pierde esta tensión opositora con mayor rapidez en comparación con la bobina de mayor inductancia

Después de un tiempo, ambas bobinas tendrán una tensión muy cerca los 0 voltios y dejan pasar la corriente plena

Cuando se tienen inductores en paralelo, se pueden reemplazar todos ellos por uno solo que nos dé las mismas características de operación del circuito; para el caso de estos componentes se cumple que, para conexiones en paralelo:

Veamos el siguiente ejemplo:

Ver video:

ARREGLOS Y COMPORTAMIENTOS DE INDUCTORES O BOBINAS EN SERIE Y PARALELO PARA APLICACIONES DC

1.9.6. APLICACIONES DE LEYES DE KIRCHOFF EN CIRCUITOS BASICOS

Estas leyes se aplican para sistemas donde interviene varias fuentes DC y cargas o resistencias, para su análisis y cálculo, está la ley de Kirchhoff para voltajes y para las corrientes; para el caso de las tensiones se tiene que:

• La suma algebraica de las caídas de tensión en la malla son cero ( 0 ); la suma algebraica de las elevaciones de tensión son igual a cero o la suma algebraica de las elevaciones de tensión son iguales a la suma algebraica de las caídas de tensión.

Para este proceso tenga presente los siguientes pasos:

· Defina el circuito cerrado a malla a analizar.

· Defina un sentido de análisis ya sea en el sentido del reloj o en contra del sentido del reloj.

· Para el caso de las resistencias, establezca la caída de tensión de acuerdo al sentido que sigue.

· El signo de la caída de tensión para el caso de las fuentes, está establecido por el polo que se encuentre en mi movimiento.

En el caso anterior, escogimos un sentido de análisis en el sentido horario, después de ello se comienza a colocar los signos de las caídas de tensión para las resistencias;; para nuestro caso si se mueve de la fuente Vf se encuentra con la resistencia R1, se sabe que las resistencias consumen tensión, por tanto a la salida de la misma tendremos menor valor de voltaje, por tanto existe una caída de tensión en la misma , por eso se le colocan un + en la entrada y un – en la salida.

Si no es encontramos con una fuente de tensión se respetan los signos que tienen sus polos y, por tanto no hay que asignarle simbología.

Para el caso de las corrientes se tiene:

· La suma algebraica de las corrientes que entran a un nodo son igual a la suma algebraica de las corrientes que salen del mismo nodo.

Para realizar un análisis de corrientes en un nodo:

· Establezca direcciones de corrientes en el circuito.

· Defina un nodo de análisis.

· Identifique las corrientes que entran al nodo y ponga sus valores en un lado de la ecuación y los valores de las corrientes que salen del otro lado de la ecuación.

Para el caso anterior, en este nodo, la corriente que entra al mismo es la If, y las que salen son las Ir3, Ir2 e Ir1. Tal como se muestra.

Para el análisis de estos circuitos se tiene en cuenta tanto el análisis de tensión por mallas como el de corriente por nodos.

Ver video:

ANALISIS DE CIRCUITOS DC CON LEYES DE OHM Y KIRCHOFF

1.10. TENSIONES Y CORRIENTES ALTERNAS

La fuente de tensión alterna genera una corriente también de tipo alterno el cual cumple la siguiente condición mostrada en la grafica

De la anterior se deduce que:

· La fuente de tensión alterna cambia de polaridad en el tiempo.

· La corriente cambia su sentido de flujo y magnitud en el tiempo.

· Tanto la corriente como el valor de voltaje tienen valores máximos y valores nulos en ciertos momentos.

La onda presentada es de tipo senoidal y en ella hay que estudiar los siguientes conceptos:

CICLO: Se define con la parte más pequeña de la gráfica que no se repite.

PERIODO ( T ) : Es la duración de un ciclo en segundos.

T = 1 / f = 1 / 60 = 0,0166 seg

FRECUENCIA ( f ): Es el número de ciclos que efectúa en un segundo ( Hertz )

f = 1/T

Para el caso del sector eléctrico colombiano, la frecuencia eléctrica es de 60 HZ o 60 ciclos /seg

AMPLITUD ( A ): Valor pico o amplitud de la onda.

FRECUENCIA ANGULAR ( w ) Es la frecuencia expresada en radianes por segundo:

w = 2 p f

En el caso del sector eléctrico colombiano que opera a 60 Hertz:

w = 2 p f = 2 p 60 = 376,991 rad/seg = 377 rad/seg

En al caso del sistema europeo que opera a 50 Hertz:

w = 2 p f = 2 p 50 = 314,16 rad/seg = 314.16 rad/seg

ANGULO DE FASE: Es la diferencia en el tiempo que existe entre la onda de voltaje o tensión y la onda de corriente, por lo general se expresa en radianes.

Como la onda es de tipo senoidal, el valor del voltaje se expresaría en forma general como

V = Vm Sen ( wt + q )

Vm: Valor de tensión pico o máximo.

t: tiempo

q: Angulo de fase en radianes

VALOR PROMEDIO

El valor promedio de una periódica es el cociente de un área y un tiempo, donde el área es la superficie entre la onda y el eje del tiempo durante un período y el tiempo es aquel que corresponde a un periodo. Las áreas en la parte superior se consideran positivas y las ubicadas en la parte inferior se consideran negativas. De acuerdo con lo anterior, el valor promedio de una sinusoide es cero, porque sobre un período las áreas positivas y negativas se cancelan al efectuarse la suma de las dos áreas.

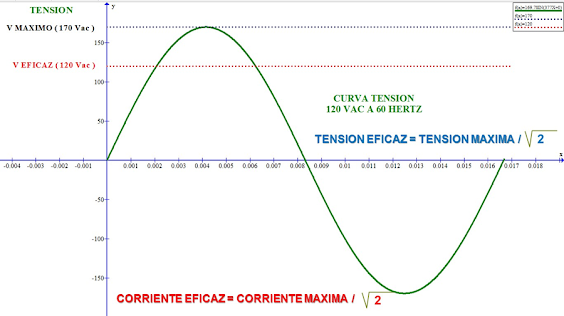
9.10.1. VALORES EFICACES O RMS

Las tensiones o corrientes eficaces se emplean en las especificaciones eléctricas de aparatos electrodomésticos. La especificación de 120 V de un secador, corresponden a valores eficaces. Lo mismo sucede con los medidores de tensión y corriente. Por definición, el valor eficaz de una tensión o corriente periódica ( V_ef o I_ef ) es el valor de tensión o corriente de corriente continua que produce el mismo valor promedio de potencia disipada en un resistor sometido a tensiones y corrientes alternos. En otras palabras, se dice que 1 amperio eficaz de corriente alterna produce los mismos efectos caloríficos de 1 amperio en corriente directa al circular por el mismo elemento resistivo.

P _promedio = ( V_ef )² / R = [ Vm ² / 2R ] è V_ef = Vmax /

P _promedio = ( I_ef )² R = [ ( R Im² ) / 2 ] è I_ef = Imax /

Entonces para nuestro sistema eléctrico a 60 Hertz, que se mide en las terminales de corriente 120 V la tensión pico de la red es:

Vmax o Vpico = V_ef * = 120 V * 1.4142 = 169.705 Voltios

Para el sistema europeo de 50 Hertz, la tensión es de 220 vac, por tanto:

Vmax o Vpico = V_ef * = 220 V * 1.4142 = 311.12 Voltios

Agregando el factor de frecuencia angular, para el sistema colombiano:

V = Vm Sen ( wt + q )

V = 120 * Sen ( 377 t + q ) = 169.705 Sen ( 377 t + q ) Voltios

Para el Sistema Europeo:

V = Vm Sen ( wt + q )

V = 220 * Sen ( 311.12 t + q ) = 311.12 Sen ( 314.16 t + q ) Voltios

Si se analizan el comportamiento de la tensión en ambas frecuencia en el lapso de 1 seg se tiene:

Si se analizan las tres líneas vivas de un sistema a 60 Hertz, se observa que las mismas no están en fase y están separadas una de la otra 120 grados.

En el caso del sistema con frecuencia de 50 Hertz:

1.10.2. SISTEMAS MONOFASICOS Y TRIFASICOS EN BAJA TENSION

Para entender los sistemas monofásicos y trifásicos de 60 o 50 Hertz, en baja tensión, analicemos como son los voltajes que llegan a nuestros hogares en ambos sistemas:

En le caso de los 60 Hertz, se poseen tres líneas vivas, llamadas: Linea 1, Linea 2 y línea 3; Fase1, Fase 2 y Fase 3; r, S y T; U, V y W; que poseen un valor de voltaje de 110 a 120 Vac, los mismo que una línea neutral con 0 voltios y la línea de protección o tierra, tal como se muestra:

Las medidas entre cualquiera de estas líneas vivas y el neutro será de 120 a 120 VAC. Si medimos la tensión entre la misma línea viva, obtendremos 0 voltios Ahora, si medimos las tensiones entre líneas vivas, vamos a tener los siguientes resultados:

,En el caso anterior, donde se emplean dos líneas vivas como alimentación, la tensión entre las mismas o resultante es la diferencia algebraica de las dos líneas senoidales, al estar desfasadas, nos da un curva de la misma frecuencia pero con valores mas altos, tal como se muestra:

Para esta nueva curva, la tensión máxima o amplitud esta alrededor de los 300 a 310 voltios y la tensión eficaz o RMS entre los 210 y 220 voltios. Dado lo anterior, podemos tener las siguientes configuraciones para cargas eléctricas en baja tensión de 60 Hertz:

Esta configuración es usada por la mayoría de los electrodomésticos de baja tensión en frecuencia de 60 Hertz. Para los sistemas trifásicos se posee:

También se pueden presentar tensiones especiales a 60 Hertz, como en el siguiente caso:

En el caso anterior, se poseen líneas vivas de 220 a 240 voltios a 60 Hertz, para electrodomésticos que usen estas tensiones, esta disponibles en algunos países. Su sistema trifásico es el siguiente:

Empleados en industria con motores AC de alta potencia.

Para el caso del sistema con frecuencia de 50 Hertz:

Para el sistema trifásico de 60 Hertz:

1.10.3. RESPUESTAS SENOIDALES DE LOS ELEMENTOS ELECTRICOS

1.10.3.1. RESPUESTA SENOIDAL DE UN RESISTOR

Si un resistor con resistencia R en ohmios se expone a una tensión V = Vm Sen ( wt + q ), el valor de la corriente que pasa por él es:

I = V/R = ( Vm / R ) Sen ( wt + q )

Se puede considerar la corriente pico Im = ( Vm / R ), por tanto la corriente que pasa por un resistor es:

I = Im Sen ( wt + q )

NOTA: Observe que los ángulos de fase q de tensión y corriente son iguales, por tanto están en fase.

La potencia instantánea disipada por un resistor varia en el tiempo, debido a que la tensión y la corriente varían también en el tiempo:

P = V*I = [ ( Vm / R ) Sen ( wt + q ) ] * [ Im Sen ( wt + q ) ] = Vm Im Sen² ( wt + q )

Pero Sen² ( x ) = ( 1 – Cos 2x )/2

è P = [ ( Vm Im ) / 2 ] – [( Vm Im ) / 2 ][ Cos ( 2wt + 2q ) ]

En la formula anterior se tiene un valor constante y un valor sinusoide con el doble de frecuencia angular y el doble de ángulo de fase. La potencia instantánea tiene un valor de cero ( 0 ) cada vez que el voltaje y corriente son cero, pero su valor nunca es negativo. El hecho de que la potencia sea siempre positiva, significa que un resistor jamás entrega potencia a un circuito.

NOTA: Recordar que potencia positiva en un dispositivo significa que la esta consumiendo; potencia negativa en un dispositivo, significa que la está entregando al circuito. La potencia promedio suministrada un resistor corresponde al primer término de la ecuación:

P _promedio = [ ( Vm Im ) / 2 ] = [ Vm ² / 2R ] = [ ( R Im² ) / 2 ]

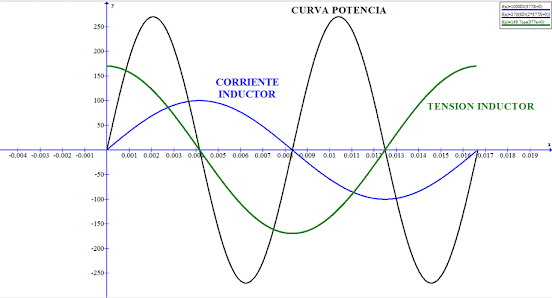
1.10.3.2. RESPUESTA SENOIDAL DE UN INDUCTOR

Hay dos formas de analizar los inductores. La primera tiene que ver si por inductor de L henrios, circula una corriente I = Im Sen ( wt + q ) al voltaje a través de ese inductor es:

V = L ( di/dt )

V = L [ Im Sen ( wt + q ) ]

V = w L Im Cos ( wt + q ) = w L Im Sen ( wt + q + 90º )

V = Vm Cos ( wt + q ) = Vm Sen ( wt + q + 90º )

De la anterior ecuación se puede deducir:

· Vm = w L Im, por tanto Im = ( Vm / w L ) . El termino w L se denomina REACTANCIA INDUCTIVA ( X_L ) y se asemeja a una resistencia, y sus unidades son ohmios ( W ). La reactancia inductiva depende de la frecuencia angular w, a mayor frecuencia, mayor efecto limitante de corriente tendrá en el inductor; por el contrario a menor frecuencia , la corriente se incrementará y cuando la frecuencia sea cero, se comportará como en corto circuito.

· Al analizar la expresión resultante del voltaje en el inductor, vemos que éste se adelanta 90º con respecto a la corriente que circula por el mismo o la corriente del inductor se atrasa con respecto al voltaje del mismo.

· En realidad, la corriente inducida de auto inducción no impide que la corriente principal pase por a bobina, sino que la misma dificulta y retarda su paso.

Para la potencia consumida por el inductor, se tiene que:

P = V*I = [ Vm Cos ( wt + q ) ]*[ Im Sen ( wt + q ) ] = Vm Im Cos ( wt + q ) Sen ( wt + q )

P = ( Vm Im / 2 ) Sen ( 2wt + 2q ) = V_ef I_ef Sen ( 2wt + 2q )

Pm = ( Vm Im / 2 ) = V_ef I_ef

Esta potencia es senoidal con un valor de frecuencia que es el doble de la frecuencia del voltaje y la corriente. Por tanto su valor promedio es cero. Por otro lado, un inductor consume energía en los tiempos cuando la potencia es positiva ( curva por encima ) y entrega energía al circuito en los tiempos en que la potencia es negativa ( curva por debajo ).

1.10.3.3. RESPUESTA SENOIDAL DE UN CAPACITOR

Si por un capacitor de C faradios, circula un voltaje V = Vm Sen ( wt + q ) la corriente a través de ese condensador es:

I = C ( dv/dt ) = C [ Vm Sen ( wt + q ) ]

I = w C Vm Cos ( wt + q ) = w C Vm Sen ( wt + q + 90º )

I = Im Cos ( wt + q ) = Im Sen ( wt + q + 90º )

De la anterior ecuación se puede deducir:

· Im = w C Vm, por tanto Vm = ( Im / w C ) . El termino ( 1 / w L ) se denomina REACTANCIA CAPACITIVA ( X_C ) y se asemeja a una resistencia, y sus unidades son W. La reactancia capacitiva depende de la frecuencia angular w, a mayor frecuencia, mayor efecto de corriente tendrá en el capacitor; por el contrario a menor frecuencia , la corriente se disminuye y cuando la frecuencia sea cero, se comportará como en un circuito abierto.

· Al analizar la expresión resultante de la corriente en el capacitor, vemos que ésta se adelanta 90º con respecto al voltaje que circula por el mismo o que el voltaje del condensador se atrasa 90º con respecto a la corriente del mismo.

· Un condensador al contrario que la bobina, facilita el paso de la corriente.

Para la potencia consumida por el inductor, se tiene que:

P = V*I = [ Vm Sen ( wt + q ) ]*[ Im Cos ( wt + q ) ] = Vm Im Cos ( wt + q ) Sen ( wt + q )

P = ( Vm Im / 2 ) Sen ( 2wt + 2q ) = V_ef I_ef Sen ( 2wt + 2q )

Pm = ( Vm Im / 2 ) = V_ef I_ef

Esta potencia es senoidal con un valor de frecuencia que es el doble de la frecuencia del voltaje y la corriente. Por tanto, su valor promedio es cero. Por otro lado, un capacitor almacena energía en los tiempos cuando la potencia es positiva ( curva por encima ) y entrega energía al circuito en los tiempos en que la potencia es negativa ( curva por debajo ).

En el aspecto de potencia, tanto el inductor como el capacitor tiene comportamientos similares.

FIN

Páginas

Seguidores del blog

martes, 29 de agosto de 2023

MODULO ELECTRICIDAD EN REFRIGERACION

No hay comentarios:

Publicar un comentario

Suscribirse a

Formulario de contacto